Issue 2
What is a Hash Table?
Reading time: 5 minutes
A hash table is a data structure that stores a collection of key/value pairs in a way that makes it very efficient to find them again later.
Why should I care?
Have you ever wanted to know:
- How does the hash map, associative array or dictionary data structure in your language work?
- When is it appropriate to use a hash table to store items?
- How do we deal with 'collisions' in a hash table?
In 5 minutes or less:
Imagine we want to store a list of users so that we can find them later using their names.

We could simply store our users in an array. When we need to find somebody later, we could loop through all of the users looking for a matching name.
That's fine when we only have 3 users. If we had thousands, though, that would be quite slow. We can do better by using a hash table.
A hash table stores items in a way that makes it much quicker to find them later, compared to looping through an array.
Creating our hash table
To use a hash table, we need a unique value for each user - this is our key. We'll use this key to store the item, and to retrieve it later.
Because it makes a nice example, we'll assume that each user has a unique name, and use that as our key. In practice, we would use something that is guaranteed to be unique like an ID.
A hash table works by storing items in buckets:
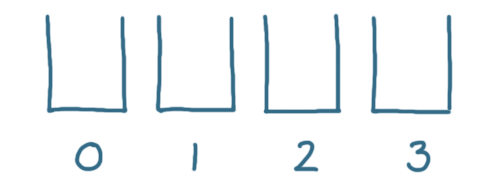
Choosing the number of buckets is a topic in itself. For the sake of a simple example, we'll use 4 buckets.
When we add a user to the hash table, we use their key to decide which bucket to store them in.
When we need to retrieve the user again, we can jump straight to the correct bucket to find them.. much quicker than checking every user in turn!
Storing items in the table
Let's store our first user, 'Ada'.
Firstly, we need to decide which bucket to store her in. That means we need to go from a string ('Ada') to a bucket number. The process of doing this is our hashing function.
We'll invent a simple hashing function for this example. Let's take each letter in the user's name and assign it a number; A=0, B=1, C=2 etc.
At the end, we can add all of the values together. The result is our hash.
For 'Ada', that's 3 - so we can store Ada in bucket 3:
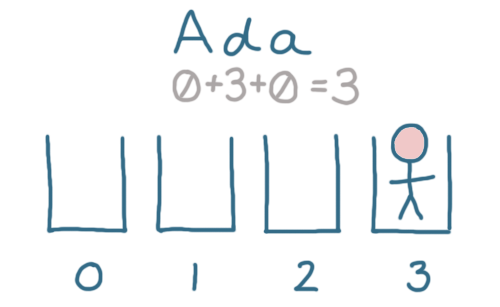
When we need to retrieve 'Ada' later, we can perform the same hashing function on her name. That will tell us to look for her in bucket number 3, no looping through arrays required.
Let's store our next user, 'Grace':
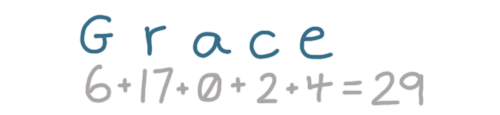
The hash for 'grace' is 29, but we don't have 29 buckets!
Storing items using just their hashed value would mean we would need a very large number of buckets. Instead, we need a way to convert the hashed value (29) to a bucket number (from 0 to 3).
A common way to do this is to divide the hash by the number of buckets, and use the remainder as the bucket number.
The remainder after dividing two numbers is called the modulus. The hash of 'grace' is 29 and we have 4 buckets. The remainder after dividing 29 by 4 is 1, so 'grace' is stored in bucket number 1.
This operation can be written ad 29 % 4 = 1, or 29 mod 4 = 1.
This is what our hash table looks like when we calculate the buckets this way:
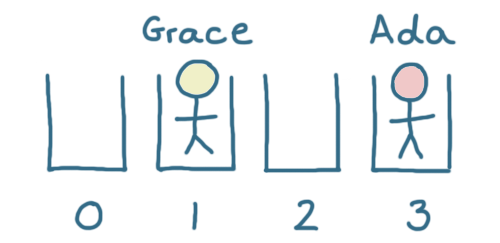
Collisions
A good hashing function aims to distribute items evenly throughout the buckets.
In practice though, we're eventually going to end up computing the same bucket for more than one item. This is called a collision.
Let's store 'Tim':
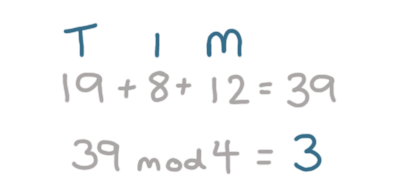
We now have two users that need to be stored in bucket 3:

There are a couple of ways to deal with this:
We could use an algorithm to keep picking new buckets until we find one that is empty, and then store our item there. The approach of only ever having one item in each bucket is called Open Addressing.
Alternatively, instead of storing just one item in each bucket, we could store a collection of items. When we find a collision using this method, we simply put both items in the same bucket.
When we need to retrieve the item later, we can still jump straight to the correct bucket. This time, though, the bucket could contain more than one item. In that case, we'll check each item in the bucket in turn, looking for the one we want.
This is called Separate Chaining, and is commonly chosen for hash table implementations.
This is one reason why good hashing functions are incredibly important for performance.
A bad hash function won't distribute items evenly, so they end up concentrated in only a small number of the available buckets.
In the worst case, where everything ends up in the same bucket, we're potentially looping through every item to find what we're looking for. That's what we are trying to avoid by using a hash table in the first place!
Want to know more?
Check out these links:
